El tic-tac que hace un columpio

Hace unos días hicimos en Twitter siguiente encuesta:

En primer lugar muchas gracias a los que participasteis, pero ahora preparamos el redoble de tambores para saber la respuesta correcta… ¡Ambos llegarán a la vez independientemente de lo que pesen! Es sorprendente como la intuición en estos casos nos juega malas pasadas y hace que nos equivoquemos. Pero, ¿cómo sabemos que nuestros dos protagonistas tardarán lo mismo en hacer su movimiento de vaivén? La respuesta la encontramos en la física de un péndulo simple, que es del que hablaremos hoy en esta publicación. Existen más tipos de péndulo, como el físico, el esférico, el doble… pero estos los dejamos para otro día porque son mucho más complicados.

¿Qué es un péndulo simple y qué tiene en común con un columpio?

Todo lo que oscila de un lado para otro es un péndulo, pero no todos son péndulos simples. Un péndulo de este tipo consiste en una masa puntual que cuelga de un hilo inextensible y con masa cero. Esto significa que idealmente toda la masa se concentra en un lugar infinitamente pequeño y que el hilo no pesa nada. Estáis en lo cierto si pensáis que esto en la vida real es imposible, pero podemos considerar que tenemos un péndulo simple siempre que se cumplan ciertas condiciones. Primero, el tamaño de la masa que cuelga tiene que ser mucho menor que la longitud del hilo que la sujeta; en segundo lugar, el hilo tiene que pesar mucho menos que la masa oscilante. Todo péndulo que cumpla estas condiciones se comportará prácticamente igual que un péndulo simple.

Si movemos ligeramente la masa hacia un lado y la soltamos, esta empezará a oscilar de un lado para otro por el efecto de la gravedad. Efectivamente, esto suena exactamente igual a lo que hace un columpio pero con palabras un poco más técnicas. El tiempo que tarda un péndulo en ir de un lado para otro se llama periodo y sorprendentemente no depende de la masa que cuelga de nuestro hilo. Esto tiene como consecuencia que tanto tú como tu amigo volveréis al punto de partida a la vez. También lo harán un elefante y un ratón, pero lo de montarlos en el columpio ya es cosa vuestra.

Con las ecuaciones del mismísimo Isaac Newton podemos calcular cuál será el periodo de un péndulo con una amplitud pequeña; este dependerá solo de la longitud de nuestro hilo y de la aceleración de la gravedad (g=9.8 m/s² en la Tierra). La expresión matemática (no huyáis que es fácil) que se obtiene es:

Por lo tanto si la longitud de nuestro hilo es 1 metro, el periodo de nuestro péndulo será aproximadamente 2 segundos. Como la masa del péndulo no aparece en esta ecuación, esto significa que el periodo de un columpio será el mismo independientemente de la masa de esa persona.

La aceleración de la gravedad, g, es otro factor que influye en el periodo. Por ejemplo, si nuestro péndulo se encontrase en la Luna, como la gravedad allí es menor, el periodo de oscilación sería mucho más largo que en la Tierra. Si queréis verlo con vuestros propios ojos, los astronautas del Apollo XIV experimentaron con un péndulo en la Luna como podéis intuir en este vídeo (por desgracia no tenían una cámara que grabase en 4K)

 
¿Y qué pasaría si la gravedad fuese cero? Para nuestra sorpresa, ¡este experimento se ha hecho en la Estación Espacial Internacional! Mirad el vídeo. En este caso, como la masa no siente una fuerza hacia abajo, el péndulo no oscila.  

Cómo usar un péndulo como un reloj.

¿Os ha impresionado todo esto? Pues esperad que aún quedan más sorpresas. Otra de las propiedades del péndulo cambió la historia para siempre. Y esto no es ninguna exageración. El insigne Galileo Galilei (1564-1642) dedicó parte de su vida a estudiar el movimiento de los péndulos y observó que el periodo es independiente de la amplitud de oscilación siempre y cuando esta no sea muy grande. Como el periodo se mantiene constante, sabemos que si una oscilación se corresponde con dos segundos, dos oscilaciones lo harán con cuatro y así hasta que nos cansemos de contar. Nuestro péndulo se acaba de convertir en un instrumento para medir el tiempo con precisión porque tenemos una equivalencia entre oscilaciones y tiempo.

Con los ojos del siglo XXI esto no nos parece demasiado impresionante, pero en el siglo XVII la precisión a la hora de medir el tiempo era fundamental para la navegación y para la estrategia bélica, entre otras cosas. Hasta 1656, los relojes tenían un error de unos 15 minutos al día, pero gracias a la tecnología desarrollada por Christiaan Huygens (1629-1695), y a sus conocimientos sobre el péndulo, el reloj pasó a tener un error de unos 15 segundos al día. Estos relojes basados en el péndulo además incluyeron una nueva aguja, la del minutero. Obviamente, antes no tenía sentido incluirla con un error tan grande.

¿Para qué otras cosas nos ha servido el péndulo?

Si os ha parecido poco, aún tenemos más. Este sencillo pero potente instrumento se usó, y se puede usar, para calcular la aceleración de la gravedad en la Tierra. Recordemos un poco las matemáticas del instituto. Partimos de la ecuación:

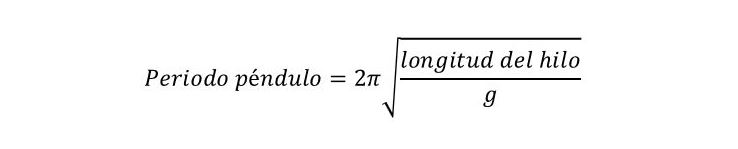
Si despejamos g, tendremos en un lado del igual el valor de la aceleración de la gravedad y en el otro el periodo del péndulo y la longitud del hilo.

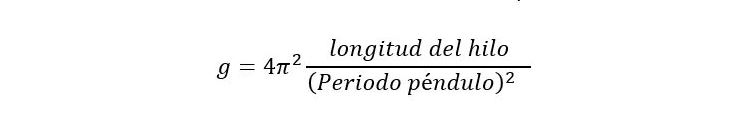
Esto significa que si sabemos la longitud del hilo de nuestro péndulo y medimos con un reloj su periodo, podemos extraer el valor de la aceleración de la gravedad terrestre. Imaginemos el experimento que aparece en la siguiente figura.

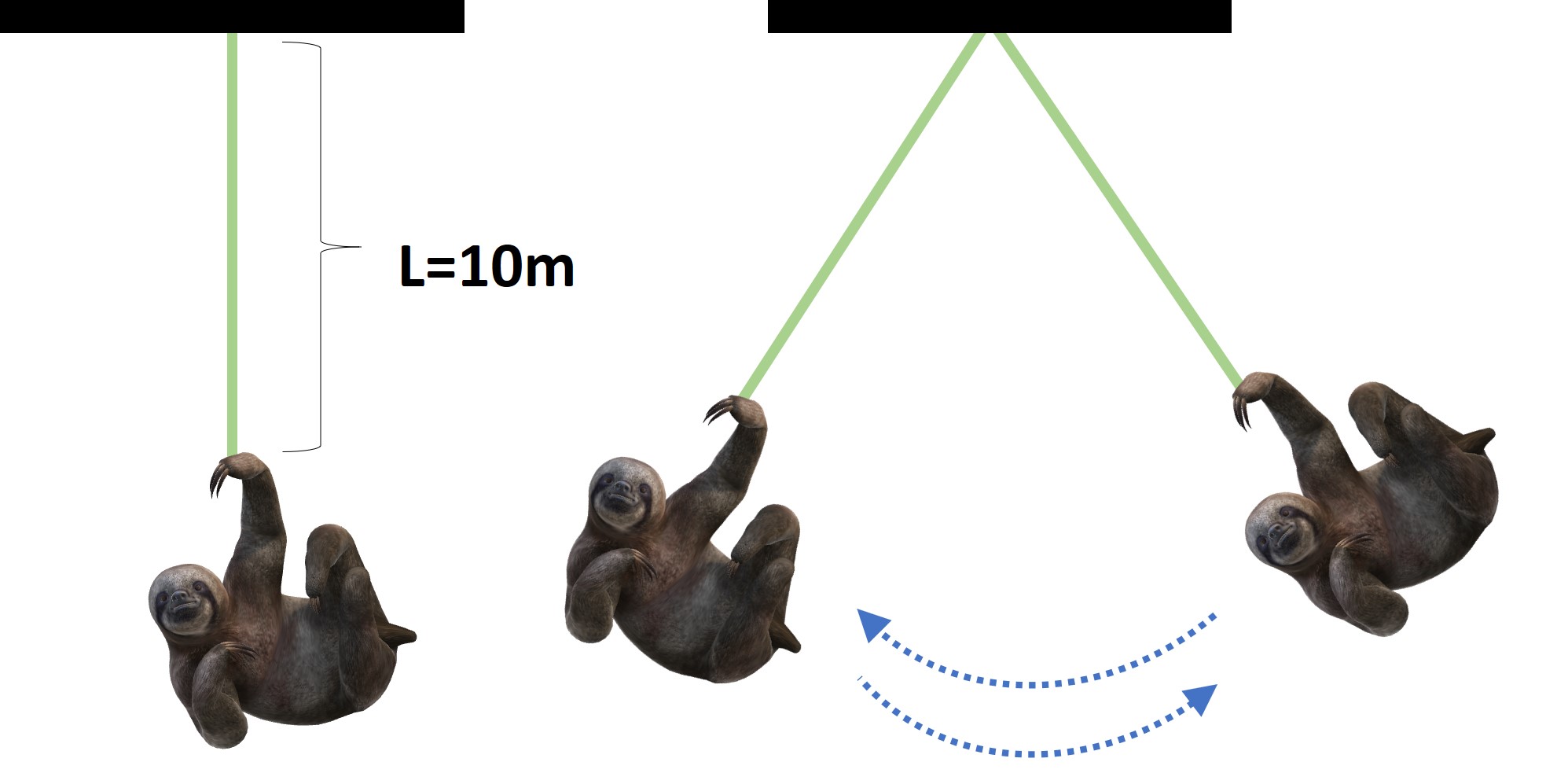
Tenemos un perezoso colgando de una liana que mide 10 metros. ¿Por qué? Porque ahora somos físicos teóricos podemos calcular lo que nos dé la gana. En un afán de diversión, el perezoso comienza a oscilar de un lado para otro y medimos que tarda 6.3 segundos en realizar una oscilación completa. Si sustituimos este periodo y la longitud de la liana en la ecuación obtenemos el valor de la aceleración de la gravedad:

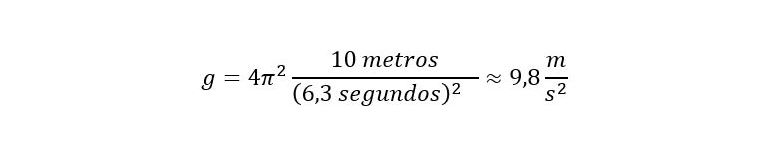
El péndulo también fue usado por Léon Foucault en 1851 para demostrar que la Tierra gira sobre sí misma, aunque en esta ocasión no se usó un péndulo simple. La idea detrás de este experimento es un poco más complicada, por lo que lo dejaremos para una futura publicación. Además, las matemáticas del péndulo, también llamado oscilador armónico, les son especialmente útiles científicos para resolver problemas que no saben hacer de otra manera.

De esta historia nos gustaría remarcar dos conclusiones. La investigación básica motivada por la curiosidad de Galileo sobre los péndulos sirvió unos años después para desarrollar mejoras en la medición precisa del tiempo, medir la aceleración de la gravedad en nuestro planeta y para verificar que este rota sobre sí mismo. No olvidemos la tremenda utilidad de la ciencia básica que a priori parece inútil. La segunda conclusión: ¡Es increíble la cantidad de cosas que se pueden hacer con una pelota atada a una cuerda!

Glosario  
Amplitud: la amplitud de un péndulo se define como la separación entre la posición de reposo y el extremo más alejado durante el movimiento. Cuando nos referimos en el texto a oscilaciones pequeñas significa que el ángulo que forma la cuerda con máxima amplitud con la vertical es pequeño.  
Péndulo físico: en el péndulo simple se considera que toda la masa que colgaba del hilo estaba concentrada en un punto infinitamente pequeño. Cuando esto no se cumple, la distribución de la masa hace que el periodo ya no sea exactamente el mismo que el del péndulo simple. A este péndulo le llamamos péndulo físico.   Péndulo esférico: hasta ahora hemos supuesto que el péndulo se movía solo en un plano, es decir, que el movimiento era de izquierda a derecha. Sin embargo, podemos encontrar péndulos que oscilan que se pueden mover de izquierda a derecha y al mismo tiempo hacia delante y hacia atrás. A este tipo de péndulo le llamamos péndulo esférico y es el que usó Foucault para demostrar que la Tierra gira sobre sí misma.    Péndulo doble: este péndulo está formado por dos péndulos simples, uno de ellos amarrado a un punto fijo mientras el segundo está amarrado al primer péndulo. Imagina que atamos un extremo de un hilo al techo y el otro a una manzana. Ahora cogemos otro hilo y atamos un extremo a una pera y el otro a la manzana. ¡Ya tenemos nuestro péndulo doble casero! Este aparente inofensivo sistema es un sistema caótico. Si quieres saber más mira en “Para saber más” para ver un ejemplo de un péndulo doble y aprender sobre la teoría del caos.

---

Para saber más

• Para los más curiosos y aventureros en el mundo de la experimentación, quizás alguno esté pensando en hacer el experimento con el columpio. En este ejemplo, el columpio se ha considerado como un péndulo simple, aunque para ciertos casos podría comportarse como un péndulo físico. Esto provocaría pequeñas diferencias en el periodo de oscilación debido a que la masa ya no se podría considerar puntual.

• Hemos aprendido que el periodo del péndulo depende de la longitud de la cuerda. Mirad qué ocurre cuando elegimos péndulos con distintas longitudes y los ponemos en fila:

• Por si alguno no se ha terminado de creer que el periodo no depende de la masa, ni de la amplitud de la oscilación (para amplitudes pequeñas), aquí tenéis todas las pruebas en un video. La demostración de la independencia de la masa os anticipo que es divertida. La podéis encontrar a partir del minuto 4:40.

El protagonista de este video, Walter Lewin, exprofesor del MIT fue acusado de acoso sexual en el año 2014 y su título de profesor emérito del MIT le fue revocado. Este caso, entre muchos otros, nos enseña que la excelencia científica no está asociada con la buena conducta personal. Nota de prensa del MIT.

• El péndulo doble es un sistema muy simple pero que contiene mucha física y muchas matemáticas. Aquí puedes ver cómo se mueve un péndulo y su conexión con la teoría del caos